在机器学习和数据挖掘中，我们经常需要知道个体间差异的大小，进而评价个体的相似性和类别（类似性度量Similarity Measurement）。采用什么样的方法计算距离是非常讲究。甚至关系到分类的正确与否。最常见的是数据分析中的相关分析，数据挖掘中的分类和聚类算法，如 K 最近邻（KNN）和 K 均值（K-Means）等等。根据数据特性的不同，可以采用不同的度量方法。一般而言，定义一个距离函数 d(x,y), 需要满足下面几个准则：

1
2
3
4
1) d(x,x) = 0                   // 到自己的距离为0
2) d(x,y) >= 0                  // 距离非负
3) d(x,y) = d(y,x)             // 对称性: 如果 A 到 B 距离是 a，那么 B 到 A 的距离也应该是 a
4) d(x,k)+ d(k,y) >= d(x,y)    // 三角形法则: (两边之和大于第三边)

这篇博客主要介绍机器学习和数据挖掘中一些常见的距离公式，包括：闵可夫斯基距离、欧几里得距离、曼哈顿距离、切比雪夫距离、马氏距离、余弦相似度、皮尔逊相关系数、汉明距离、杰卡德相似系数、编辑距离、DTW 距离、KL 散度。

数值点之间的距离

闵可夫斯基距离（Minkowski distance）是衡量数值点之间距离的一种非常常见的方法，假设数值点 P 和 Q 坐标如下：

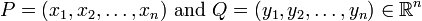
那么，闵可夫斯基距离定义为：

img

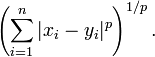
该距离最常用的 p 是 2 和 1, 前者是欧几里得距离（Euclidean distance），后者是曼哈顿距离（Manhattan distance）。假设在曼哈顿街区乘坐出租车从 P 点到 Q 点，白色表示高楼大厦，灰色表示街道：

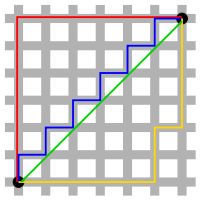
绿色的斜线表示欧几里得距离，在现实中是不可能的。其他三条折线表示了曼哈顿距离，这三条折线的长度是相等的。

当 p 趋近于无穷大时，闵可夫斯基距离转化成切比雪夫距离（Chebyshev distance）：

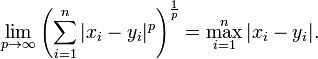
我们知道平面上到原点欧几里得距离（p = 2）为 1 的点所组成的形状是一个圆，当 p 取其他数值的时候呢？

注意，当 p < 1 时，闵可夫斯基距离不再符合三角形法则，举个例子：当 p < 1, (0,0) 到 (1,1) 的距离等于 $(1+1)^{1/p} > 2$, 而 (0,1) 到这两个点的距离都是 1。

闵可夫斯基距离比较直观，但是它与数据的分布无关，具有一定的局限性，如果 x 方向的幅值远远大于 y 方向的值，这个距离公式就会过度放大 x 维度的作用。所以，在计算距离之前，我们可能还需要对数据进行 z-transform 处理，即减去均值，除以标准差：

$$(x_1,y_1)\mapsto(\frac{x_1-\mu_x}{\sigma_x},\frac{y_1-\mu_y}{\sigma_y})$$

$\mu$ : 该维度上的均值
$\sigma$: 该维度上的标准差

可以看到，上述处理开始体现数据的统计特性了。这种方法在假设数据各个维度不相关的情况下利用数据分布的特性计算出不同的距离。如果维度相互之间数据相关（例如：身高较高的信息很有可能会带来体重较重的信息，因为两者是有关联的），这时候就要用到马氏距离（Mahalanobis distance）了。

欧氏距离(Euclidean Distance)

欧氏距离是最易于理解的一种距离计算方法，源自欧几里得几何中两点间的距离公式。

(1)二维平面上两点a$(x_1,y_1)$与b$(x_2,y_2)$间的欧氏距离：

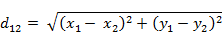
(2)两个n维向量a$(x_11,x_12,…,x_1n)$与 b$(x_21,x_22,…,x_2n)$间的欧氏距离：

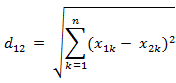
(3)也能够用表示成向量运算的形式：

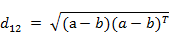
(4)Matlab计算欧氏距离

Matlab计算距离主要使用pdist函数。
若X是一个M×N的矩阵。则pdist(X)将X矩阵M行的每一行作为一个N维向量。然后计算这M个向量两两间的距离。
样例：计算向量(0,0)、(1,0)、(0,2)两两间的欧式距离

1
2
3
4
5
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'euclidean') %大家能够去查一查pdist的參数
结果：
D =
    1.0000    2.0000    2.2361

曼哈顿距离(Manhattan Distance)

从名字就能够猜出这样的距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源， 曼哈顿距离也称为城市街区距离(City Block distance)。

(1)二维平面两点a:$(x_1,y_1)$与b:$(x_2,y_2)$间的曼哈顿距离

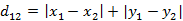
(2)两个n维向量a$(x_{11},x_{12},…,x_{1n})$与 b$(x_{21},x_{22},…,x_{2n})$间的曼哈顿距离

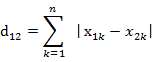
(3) Matlab计算曼哈顿距离

样例：计算向量(0,0)、(1,0)、(0,2)、(2,2)两两间的曼哈顿距离

1
2
3
4
5
X = [0 0 ; 1 0 ; 0 2 ; 2 2];
D = pdist(X,'cityblock')
结果：
D =
     1     2     4     3     3     2

切比雪夫距离 ( Chebyshev Distance )

国际象棋玩过么？国王走一步能够移动到相邻的8个方格中的随意一个。那么国王从格子$(x_1,y_1)$走到格子$(x_2,y_2)$最少须要多少步？自己走走试试。你会发现最少步数总是$max( | x_2-x_1 | , | y_2-y_1 | )$ 步 。有一种类似的一种距离度量方法叫切比雪夫距离。

(1)二维平面两点a$(x_1,y_1)$与b$(x_2,y_2)$间的切比雪夫距离

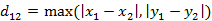
(2)两个n维向量a$(x_{11},x_{12},…,x_{1n})$与 b$(x_{21},x_{22},…,x_{2n})$间的切比雪夫距离

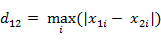
　　这个公式的还有一种等价形式是

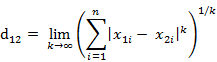
看不出两个公式是等价的？提示一下：试试用放缩法和夹逼法则来证明。

(3)Matlab计算切比雪夫距离

样例：计算向量(0,0)、(1,0)、(0,2)两两间的切比雪夫距离

1
2
3
4
5
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'chebychev')
结果：
D =
     1     2     2

闵可夫斯基距离(Minkowski Distance)

闵氏距离不是一种距离。而是一组距离的定义，上文说的几个距离都是属于闵可夫斯基距离的。

(1) 闵氏距离的定义

两个n维变量a$(x_{11},x_{12},…,x_{1n})$与 b$(x_{21},x_{22},…,x_{2n})$间的闵可夫斯基距离定义为：

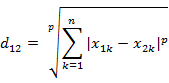
当中p是一个变參数。
当p=1时，就是曼哈顿距离
当p=2时，就是欧氏距离
当p→∞时，就是切比雪夫距离

依据变參数的不同。闵氏距离能够表示一类的距离。

(2)闵氏距离的缺点

闵氏距离。包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。

举个样例：
二维样本(身高,体重)，当中身高范围是[150,190]，体重范围是[50,60]，有三个样本：a(180,50)，b(190,50)，c(180,60)。
那么a与b之间的闵氏距离（不管是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c之间的闵氏距离，可是身高的10cm真的等价于体重的10kg么？因此用闵氏距离来衡量这些样本间的类似度非常有问题。

简单说来。闵氏距离的缺点主要有两个：

  • 将各个分量的量纲(scale)，也就是“单位”当作相同的看待了。
  • 没有考虑各个分量的分布（期望，方差等)可能是不同的。

(3)Matlab计算闵氏距离

样例：计算向量(0,0)、(1,0)、(0,2)两两间的闵氏距离（以变參数为2的欧氏距离为例）

1
2
3
4
5
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X,'minkowski',2)
结果：
D =
    1.0000    2.0000    2.2361

标准化欧氏距离 (Standardized Euclidean distance )

(1)标准欧氏距离的定义

标准化欧氏距离是针对简单欧氏距离的缺点而作的一种改进方案。
标准欧氏距离的思路：既然数据各维分量的分布不一样。那先将各个分量都“标准化”到均值、方差相等。
均值和方差标准化到多少呢？这里先复习点统计学知识吧。如果样本集X的均值(mean)为m，标准差(standard deviation)为s，那么X的“标准化变量”表示为：
X∗=X−ms
标准化变量的数学期望为0。方差为1。因此样本集的标准化过程(standardization)用公式描写叙述就是：
标准化后的值 = ( 标准化前的值 － 分量的均值 ) /分量的标准差
经过简单的推导就能够得到两个n维向量a$(x_{11},x_{12},…,x_{1n})$与 b$(x_{21},x_{22},…,x_{2n})$间的标准化欧氏距离的公式：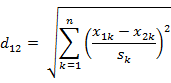

如果将方差的倒数看成是一个权重，这个公式能够看成是一种加权欧氏距离(Weighted Euclidean distance)。

(2)Matlab计算标准化欧氏距离

样例：计算向量(0,0)、(1,0)、(0,2)两两间的标准化欧氏距离 (如果两个分量的标准差分别为0.5和1)

1
2
3
4
5
X = [0 0 ; 1 0 ; 0 2]
D = pdist(X, 'seuclidean',[0.5,1])
结果：
D =
    2.0000    2.0000    2.8284

马氏距离(Mahalanobis Distance)

马氏距离(Mahalanobis distance)是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的，表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是，它考虑到各种特性之间的联系（例如：一条关于身高的信息会带来一条关于体重的信息，因为两者是有关联的），并且是尺度无关的(scale-invariant)，即独立于测量尺度。

####（1）马氏距离定义

有M个样本向量$x_1··· X_m$，协方差矩阵记为S，均值记为向量μ，则当中样本向量X到μ的马氏距离表示为：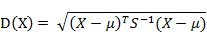

而当中向量Xi与Xj之间的马氏距离定义为：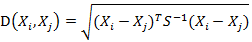

若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：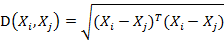

也就是欧氏距离了。
若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离。

(2)马氏距离的优缺点：

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关，由标准化数据和中心化数据(即原始数据与均值之差）计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。

缺点：它的缺点是夸大了变化微小的变量的作用。

(3) Matlab计算

样例：计算(1,2)、(1,3)、(2,2)、(3,1)两两之间的马氏距离

1
2
3
4
5
X = [1 2; 1 3; 2 2; 3 1]
Y = pdist(X,'mahalanobis')
结果：
Y =
    2.3452    2.0000    2.3452    1.2247    2.4495    1.2247

理解

考虑下面这张图，椭圆表示等高线，从欧几里得的距离来算，绿黑距离大于红黑距离，但是从马氏距离，结果恰好相反：

img

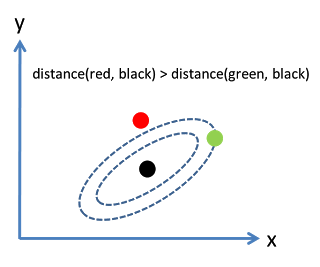
马氏距离实际上是利用 Cholesky transformation 来消除不同维度之间的相关性和尺度不同的性质。假设样本点（列向量）之间的协方差对称矩阵是 $\Sigma$ ， 通过 Cholesky Decomposition（实际上是对称矩阵 LU 分解的一种特殊形式，可参考博客）可以转化为下三角矩阵和上三角矩阵的乘积： $\Sigma=LL^T$ 。消除不同维度之间的相关性和尺度不同，只需要对样本点 x 做如下处理：$z=L^{-1}(x-\mu)$ 。处理之后的欧几里得距离就是原样本的马氏距离：为了书写方便，这里求马氏距离的平方）：

img

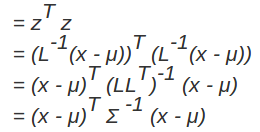
下图蓝色表示原样本点的分布，两颗红星坐标分别是（3, 3），（2, -2）:

img

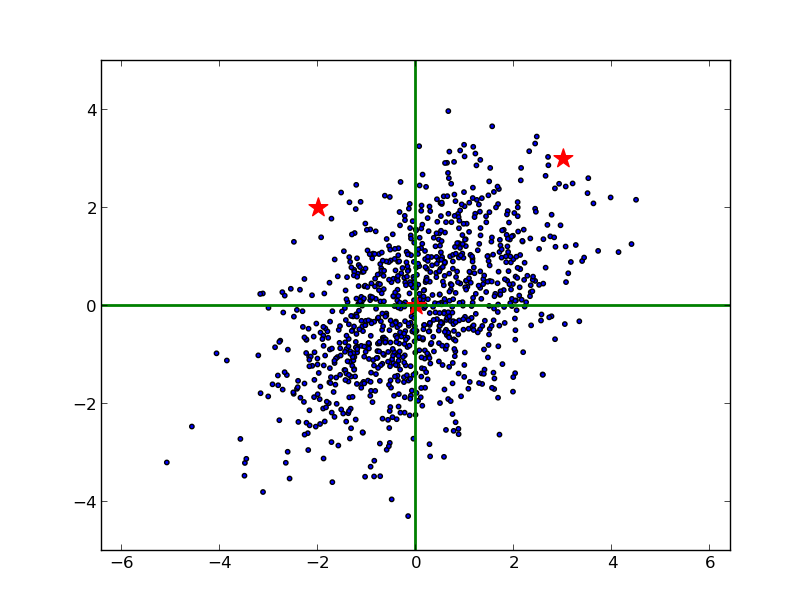
由于 x， y 方向的尺度不同，不能单纯用欧几里得的方法测量它们到原点的距离。并且，由于 x 和 y 是相关的（大致可以看出斜向右上），也不能简单地在 x 和 y 方向上分别减去均值，除以标准差。最恰当的方法是对原始数据进行 Cholesky 变换，即求马氏距离（可以看到，右边的红星离原点较近）：

img

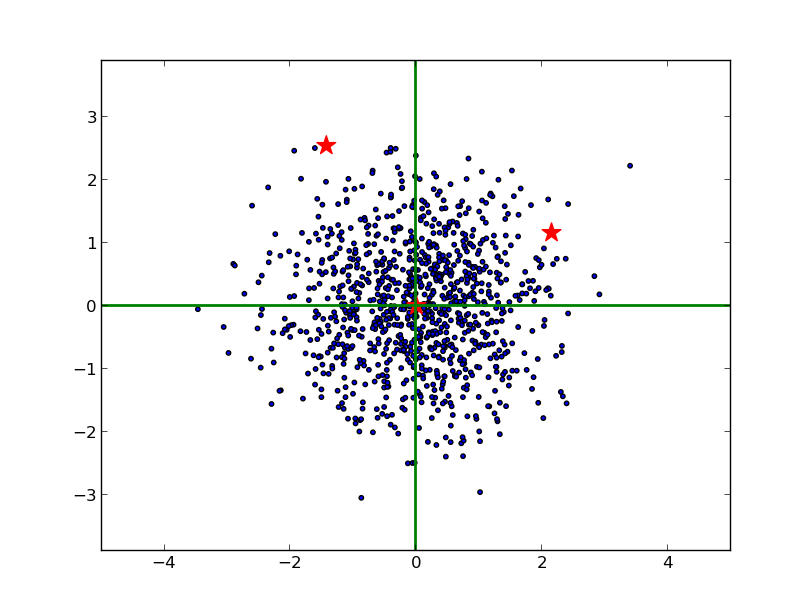
将上面两个图的绘制代码和求马氏距离的代码贴在这里，以备以后查阅：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
 1 # -*- coding=utf-8 -*-
 2 
 3 # code related at: http://www.cnblogs.com/daniel-D/
 4 
 5 import numpy as np
 6 import pylab as pl
 7 import scipy.spatial.distance as dist
 8 
 9 
10 def plotSamples(x, y, z=None):
11 
12     stars = np.matrix([[3., -2., 0.], [3., 2., 0.]])
13     if z is not None:
14         x, y = z * np.matrix([x, y])
15         stars = z * stars
16 
17     pl.scatter(x, y, s=10)    # 画 gaussian 随机点
18     pl.scatter(np.array(stars[0]), np.array(stars[1]), s=200, marker='*', color='r')  # 画三个指定点
19     pl.axhline(linewidth=2, color='g') # 画 x 轴
20     pl.axvline(linewidth=2, color='g')  # 画 y 轴
21 
22     pl.axis('equal')
23     pl.axis([-5, 5, -5, 5])
24     pl.show()
25 
26 
27 # 产生高斯分布的随机点
28 mean = [0, 0]      # 平均值
29 cov = [[2, 1], [1, 2]]   # 协方差
30 x, y = np.random.multivariate_normal(mean, cov, 1000).T
31 plotSamples(x, y)
32 
33 covMat = np.matrix(np.cov(x, y))    # 求 x 与 y 的协方差矩阵
34 Z = np.linalg.cholesky(covMat).I  # 仿射矩阵
35 plotSamples(x, y, Z)
36 
37 # 求马氏距离 
38 print '\n到原点的马氏距离分别是：'
39 print dist.mahalanobis([0,0], [3,3], covMat.I), dist.mahalanobis([0,0], [-2,2], covMat.I)
40 
41 # 求变换后的欧几里得距离
42 dots = (Z * np.matrix([[3, -2, 0], [3, 2, 0]])).T
43 print '\n变换后到原点的欧几里得距离分别是：'
44 print dist.minkowski([0, 0], np.array(dots[0]), 2), dist.minkowski([0, 0], p.array(dots[1]),2)

马氏距离的变换和 PCA 分解的白化处理颇有异曲同工之妙，不同之处在于：就二维来看，PCA 是将数据主成分旋转到 x 轴（正交矩阵的酉变换），再在尺度上缩放（对角矩阵），实现尺度相同。而马氏距离的 L逆矩阵是一个下三角，先在 x 和 y 方向进行缩放，再在 y 方向进行错切（想象矩形变平行四边形），总体来说是一个没有旋转的仿射变换。

夹角余弦(Cosine)

几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异。

(1)在二维空间中向量a$(x_1,y_1)$与向量b$(x_2,y_2)$的夹角余弦公式：

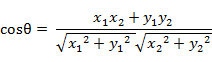
(2) 两个n维样本点a(x_11,x_12,…,x_1n)和b(x_21,x_22,…,x_2n)的夹角余弦：


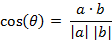
类似的，对于两个n维样本点a(x_11,x_12,…,x_1n)和b(x_21,x_22,…,x_2n)，能够使用类似于夹角余弦的概念来衡量它们间的类似程度。
　　即：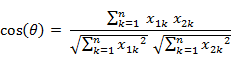

夹角余弦取值范围为[−1,1]。夹角余弦越大表示两个向量的夹角越小，夹角余弦越小表示两向量的夹角越大。
当两个向量的方向重合时夹角余弦取最大值1，当两个向量的方向全然相反夹角余弦取最小值-1。

(3)Matlab计算夹角余弦

样例：计算(1,0)、(1,1.732)、(−1,0)两两间的夹角余弦

1
2
3
4
5
X = [1 0 ; 1 1.732 ; -1 0]
D = 1- pdist(X, 'cosine')  % Matlab中的pdist(X, 'cosine')得到的是1减夹角余弦的值
结果：
D =
    0.5000   -1.0000   -0.5000

分类数据点之间的距离

汉明距离(Hamming distance)

(1)汉明距离的定义

两个等长字符串$s_1$与$s_2$之间的汉明距离定义为将当中一个变为另外一个所须要作的最小替换次数。比如字符串“1111”与“1001”之间的汉明距离为2。
应用：信息编码（为了增强容错性。应使得编码间的最小汉明距离尽可能大）。

(2)Matlab计算汉明距离

Matlab中2个向量之间的汉明距离的定义为2个向量不同的分量所占的百分比。
样例：计算向量(0,0,0)、(0,0,1)、(0,1,0)、(1,0,0)、(0,1,1)两两间的汉明距离

1
2
3
4
5
X = [0 0 0 ; 0 0 1 ; 0 1 0 ; 1 0 0 ; 0 1 1];
D = pdist(X,'hamming')
结果：
D =
    0.3333    0.3333    0.3333    0.6667    0.6667    0.6667    0.3333    0.6667    0.3333    1.0000

在一些情况下，某些特定的值相等并不能代表什么。举个例子，用 1 表示用户看过该电影，用 0 表示用户没有看过，那么用户看电影的的信息就可用 0,1 表示成一个序列。考虑到电影基数非常庞大，用户看过的电影只占其中非常小的一部分，如果两个用户都没有看过某一部电影（两个都是 0），并不能说明两者相似。反而言之，如果两个用户都看过某一部电影（序列中都是 1），则说明用户有很大的相似度。在这个例子中，序列中等于 1 所占的权重应该远远大于 0 的权重，这就引出下面要说的杰卡德相似系数（Jaccard similarity）。

在上面的例子中，用 M11 表示两个用户都看过的电影数目，M10 表示用户 A 看过，用户 B 没看过的电影数目，M01 表示用户 A 没看过，用户 B 看过的电影数目，M00 表示两个用户都没有看过的电影数目。Jaccard 相似性系数可以表示为：

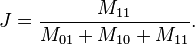
Jaccard similarity 还可以用集合的公式来表达。

如果分类数值点是用树形结构来表示的，它们的相似性可以用相同路径的长度来表示，比如，“/product/spot/ballgame/basketball” 离“product/spot/ballgame/soccer/shoes” 的距离小于到 “/product/luxury/handbags” 的距离，以为前者相同父节点路径更长。

杰卡德类似系数(Jaccard similarity coefficient)

(1) 杰卡德类似系数

两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德类似系数。用符号J(A,B)表示。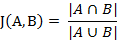

杰卡德类似系数是衡量两个集合的类似度一种指标。

(2) 杰卡德距离

与杰卡德类似系数相反的概念是杰卡德距离(Jaccard distance)。
杰卡德距离可用例如以下公式表示：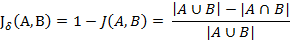

　　杰卡德距离用两个集合中不同元素占全部元素的比例来衡量两个集合的区分度。

(3) 杰卡德类似系数与杰卡德距离的应用

可将杰卡德类似系数用在衡量样本的类似度上。

样本A与样本B是两个n维向量，并且全部维度的取值都是0或1。比如：A(0111)和B(1011)。
我们将样本看成是一个集合，1表示集合包括该元素，0表示集合不包括该元素。
p ：样本A与B都是1的维度的个数
q ：样本A是1，样本B是0的维度的个数
r ：样本A是0，样本B是1的维度的个数
s ：样本A与B都是0的维度的个数
这里p+q+r可理解为A与B的并集的元素个数。而p是A与B的交集的元素个数。
而样本A与B的杰卡德距离表示为：

(4)Matlab 计算杰卡德距离

Matlab的pdist函数定义的杰卡德距离跟我这里的定义有一些区别，Matlab中将其定义为不同的维度的个数占“非全零维度”的比例。
样例：计算(1,1,0)、(1,−1,0)、(−1,1,0)两两之间的杰卡德距离

1
2
3
4
5
X = [1 1 0; 1 -1 0; -1 1 0]
D = pdist( X , 'jaccard')
结果
D =
0.5000    0.5000    1.0000

序列之间的距离(字符串、时序)

上一小节我们知道，汉明距离可以度量两个长度相同的字符串之间的相似度，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离（Edit distance, Levenshtein distance）等算法。编辑距离是指两个字串之间，由一个转成另一个所需的最少编辑操作次数。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。编辑距离求的是最少编辑次数，这是一个动态规划的问题，有兴趣的同学可以自己研究研究。

时间序列是序列之间距离的另外一个例子。DTW 距离（Dynamic Time Warp）是序列信号在时间或者速度上不匹配的时候一种衡量相似度的方法。神马意思？举个例子，两份原本一样声音样本A、B都说了“你好”，A在时间上发生了扭曲，“你”这个音延长了几秒。最后A:“你~~~~~~~好”，B：“你好”。DTW正是这样一种可以用来匹配A、B之间的最短距离的算法。

DTW 距离在保持信号先后顺序的限制下对时间信号进行“膨胀”或者“收缩”，找到最优的匹配，与编辑距离相似，这其实也是一个动态规划的问题:

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#!/usr/bin/python2
# -*- coding:UTF-8 -*-
# code related at: http://blog.mckelv.in/articles/1453.html
 
import sys
 
distance = lambda a,b : 0 if a==b else 1
 
def dtw(sa,sb):
    '''
    >>>dtw(u"干啦今今今今今天天气气气气气好好好好啊啊啊", u"今天天气好好啊")
    2
    '''
    MAX_COST = 1<<32
    #初始化一个len(sb) 行(i)，len(sa)列(j)的二维矩阵
    len_sa = len(sa)
    len_sb = len(sb)
    # BUG:这样是错误的(浅拷贝): dtw_array = [[MAX_COST]*len(sa)]*len(sb)
    dtw_array = [[MAX_COST for i in range(len_sa)] for j in range(len_sb)]
    dtw_array[0][0] = distance(sa[0],sb[0])
    for i in xrange(0, len_sb):
        for j in xrange(0, len_sa):
            if i+j==0:
                continue
            nb = []
            if i > 0: nb.append(dtw_array[i-1][j])
            if j > 0: nb.append(dtw_array[i][j-1])
            if i > 0 and j > 0: nb.append(dtw_array[i-1][j-1])
            min_route = min(nb)
            cost = distance(sa[j],sb[i])
            dtw_array[i][j] = cost + min_route
    return dtw_array[len_sb-1][len_sa-1]
 
 
def main(argv):
    s1 = u'干啦今今今今今天天气气气气气好好好好啊啊啊'
    s2 = u'今天天气好好啊'
    d = dtw(s1, s2)
    print d
    return 0
 
if __name__ == '__main__':
    sys.exit(main(sys.argv))

相关系数 ( Correlation coefficient )与相关距离(Correlation distance)

(1) 相关系数的定义


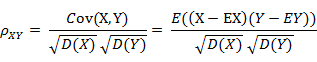
相关系数是衡量随机变量X与Y相关程度的一种方法，相关系数的取值范围是[−1,1]。相关系数的绝对值越大，则表明X与Y相关度越高。
当X与Y线性相关时，相关系数取值为1（正线性相关）或-1（负线性相关）。

(2)相关距离的定义

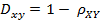
(3)Matlab计算(1,2,3,4)与(3,8,7,6)之间的相关系数与相关距离

1
2
3
4
5
6
7
8
9
10
11
12
X = [1 2 3 4 ; 3 8 7 6]
C = corrcoef( X' )   %将返回相关系数矩阵
D = pdist( X , 'correlation')
结果：
C =
    1.0000    0.4781

    0.4781    1.0000
D =
0.5219

      当中0.4781就是相关系数，0.5219是相关距离。

混合分类数据点与数字数据点之间的距离

当数据点包含数值属性和分类属性的混合时，我们可以计算每个组的距离，然后将每个距离度量作为一个单独的维度(数值)。

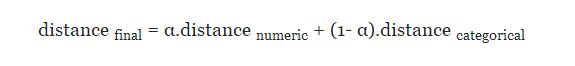
概率分布之间的距离

前面我们谈论的都是两个数值点之间的距离，实际上两个概率分布之间的距离是可以测量的。在统计学里面经常需要测量两组样本分布之间的距离，进而判断出它们是否出自同一个 population，常见的方法有卡方检验（Chi-Square）和 KL 散度（ KL-Divergence），下面说一说 KL 散度吧。

先从信息熵说起，假设一篇文章的标题叫做“黑洞到底吃什么”，包含词语分别是 {黑洞, 到底, 吃什么}, 我们现在要根据一个词语推测这篇文章的类别。哪个词语给予我们的信息最多？很容易就知道是“黑洞”，因为“黑洞”这个词语在所有的文档中出现的概率太低啦，一旦出现，就表明这篇文章很可能是在讲科普知识。而其他两个词语“到底”和“吃什么”出现的概率很高，给予我们的信息反而越少。如何用一个函数 h(x) 表示词语给予的信息量呢？第一，肯定是与 p(x) 相关，并且是负相关。第二，假设 x 和 y 是独立的（黑洞和宇宙不相互独立，谈到黑洞必然会说宇宙）,即 p(x,y) = p(x)p(y), 那么获得的信息也是叠加的，即 h(x, y) = h(x) + h(y)。满足这两个条件的函数肯定是负对数形式：

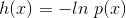
对假设一个发送者要将随机变量 X 产生的一长串随机值传送给接收者， 接受者获得的平均信息量就是求它的数学期望：

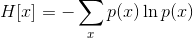
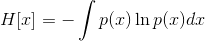
这就是熵的概念。另外一个重要特点是，熵的大小与字符平均最短编码长度是一样的（shannon）。设有一个未知的分布 p(x), 而 q(x) 是我们所获得的一个对 p(x) 的近似，按照 q(x) 对该随机变量的各个值进行编码，平均长度比按照真实分布的 p(x) 进行编码要额外长一些，多出来的长度这就是 KL 散度（之所以不说距离，是因为不满足对称性和三角形法则），即：

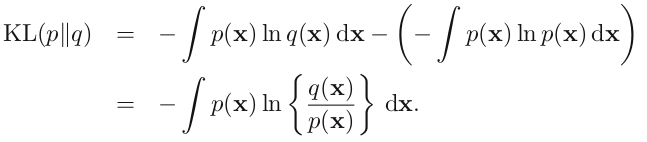
KL 散度又叫相对熵（relative entropy）。了解机器学习的童鞋应该都知道，在 Softmax 回归（或者 Logistic 回归），最后的输出节点上的值表示这个样本分到该类的概率，这就是一个概率分布。对于一个带有标签的样本，我们期望的概率分布是：分到标签类的概率是 1， 其他类概率是 0。但是理想很丰满，现实很骨感，我们不可能得到完美的概率输出，能做的就是尽量减小总样本的 KL 散度之和（目标函数）。这就是 Softmax 回归或者 Logistic 回归中 Cost function 的优化过程啦。（PS：因为概率和为 1，一般的 logistic 二分类的图只画了一个输出节点，隐藏了另外一个）

向量内积

向量内积是线性代数里最为常见的计算，实际上它还是一种有效并且直观的相似性测量手段。向量内积的定义如下：

$$Inner(x,y)=\langle x,y\rangle=\sum_ix_iy_i$$

直观的解释是：如果 x 高的地方 y 也比较高， x 低的地方 y 也比较低，那么整体的内积是偏大的，也就是说 x 和 y 是相似的。举个例子，在一段长的序列信号 A 中寻找哪一段与短序列信号 a 最匹配，只需要将 a 从 A 信号开头逐个向后平移，每次平移做一次内积，内积最大的相似度最大。信号处理中 DFT 和 DCT 也是基于这种内积运算计算出不同频域内的信号组分（DFT 和 DCT 是正交标准基，也可以看做投影）。向量和信号都是离散值，如果是连续的函数值，比如求区间[-1, 1] 两个函数之间的相似度，同样也可以得到（系数）组分，这种方法可以应用于多项式逼近连续函数，也可以用到连续函数逼近离散样本点（最小二乘问题，OLS coefficients）中，扯得有点远了- -!。

向量内积的结果是没有界限的，一种解决办法是除以长度之后再求内积，这就是应用十分广泛的余弦相似度（Cosine similarity）：

$$CosSim(x,y)=\frac{\sum_ix_iy_i}{\sqrt{\sum_ix_i^2}\sqrt{\sum_iy_i^2}}=\frac{\langle x,y\rangle}{||x||||y||}$$

余弦相似度与向量的幅值无关，只与向量的方向相关，在文档相似度（TF-IDF）和图片相似性（histogram）计算上都有它的身影。需要注意一点的是，余弦相似度受到向量的平移影响，上式如果将 x 平移到 x+1, 余弦值就会改变。怎样才能实现平移不变性？这就是下面要说的皮尔逊相关系数（Pearson correlation），有时候也直接叫相关系数:

$$\begin{align}Corr(x,y)&=\frac{\sum_i(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum(x_i-\bar{x})^2}\sqrt{\sum(y_i-\bar{y})^2}}\&=\frac{\langle x-\bar{x},y-\bar{y}\rangle}{||x-\bar{x}||||y-\bar{y}||}\&=CosSim(x-\bar{x},y-\bar{y})\end{align}$$

皮尔逊相关系数具有平移不变性和尺度不变性，计算出了两个向量（维度）的相关性。不过，一般我们在谈论相关系数的时候，将 x 与 y 对应位置的两个数值看作一个样本点，皮尔逊系数用来表示这些样本点分布的相关性。

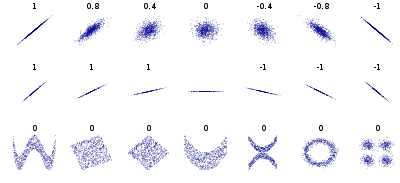
由于皮尔逊系数具有的良好性质，在各个领域都应用广泛，例如，在推荐系统根据为某一用户查找喜好相似的用户，优点是可以不受每个用户评分标准不同和观看影片数量不一样的影响。

参考：

数学中几种经常使用的距离

漫谈:机器学习中距离和相似性的度量方法

Machine Learning: Measuring Similarity and Distance

Computing and Visualizing Dynamic Time Warping Alignments in R: The dtw Package