虚数i真的存在吗?
存在是一个哲学问题,自然数1、2、3、4是否存在?它们没有现实对应物,但是会在一个香蕉、两个苹果中被探测到,那么到底算是存在还是不存在呢?虚数呢?虚数i 是不是真实存在的,这真的不是一个显而易见的问题,而且按照中国教材的编写顺序,数学教育中第一次出现和现实脱离的概念大概就是虚数,这应该是教育中一次很好阐述数学思想的时间和机会。
1 数系的扩展
数系的扩展过程直观上来说就是给数轴“填坑”的过程。
1.1 整数
自然数出现是挺自然的,小孩自然就知道了一个苹果、两个香蕉,去掉苹果香蕉,剩下1、2,就是数学的初步抽象。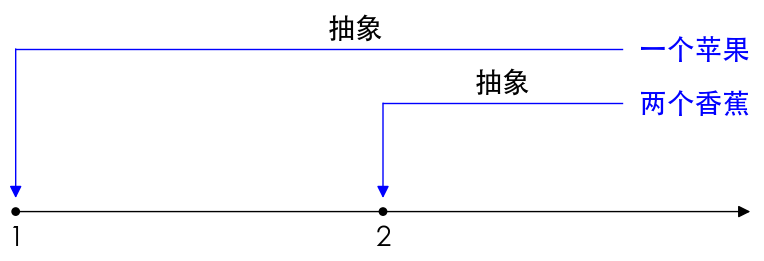
这个时候数轴上有没有坑啊?当然有了。

1.2 有理数
数轴上还有坑吗?当然有。
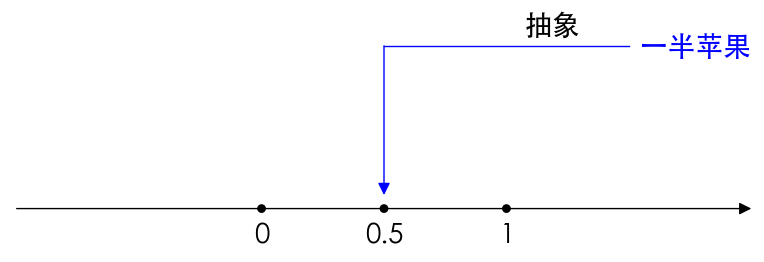
整数与整数的比就是有理数。有理数这个名字翻译的有点意思,英文是rational number,明明是可以翻译为”比例数“(就是整数和整数的比),让我以前一直觉得后面出现的无理数好粗鲁。
1.3 无理数
有了整数和有理数之后,数轴还有没有坑?这个问题真的不那么显然了。任何两个有理数,比如说0.5和0.7,平均值 $\frac{0.5+0.7}{2}=0.6$还是有理数,不论这两个有理数之间隔得有多近。就是说任何两个有理数之间不可能相邻,他们之间必定还有有理数。看起来就仿佛在数轴上连绵不断。
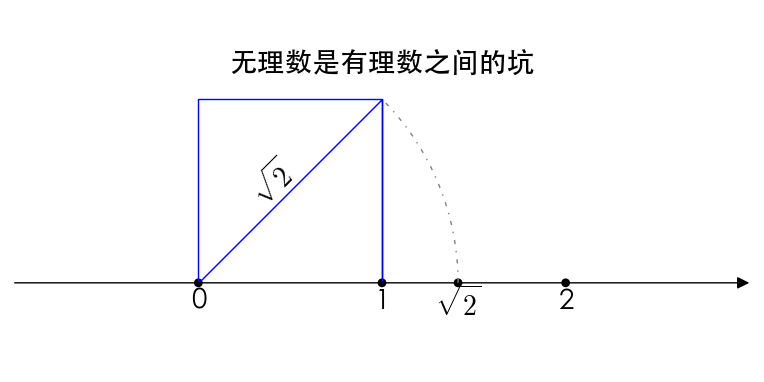
$\sqrt2$是第一个发现的无理数,因此还引发了第一次数学危机。我们回头来看看 $\sqrt 2$ ,不通过证明我们还真没有办法说明它不是有理数,实际上大多数时候,无理数都需要证明,比如 e,$\pi$ 这样有名的无理数,在证明之前我们并不知道它是有理数还是无理数,而且证明难度还不小。
这里稍微提一下,其实无理数的数目要比有理数多得多。我们知道,有理数是无限循环小数,无理数是无限不循环小数。我们直观的来想象一下,我们面前有10个球,上面标着0到9的数字,我们闭着眼睛随机抓取一个球,球上标注的数字就作为小数点后面的第一个数字,把球放回去再抓,就作为第二个数字,无限的抓下去,生成有理数的概率为0(概率学里面,概率为0不并意味着事件完全不可能发生,而是说几乎不可能)。
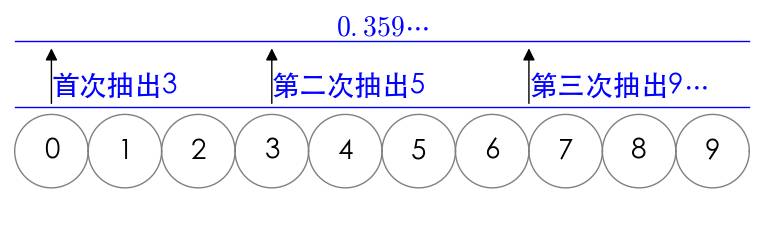
其实无理数才是常态,有理数才是没有道理的数。
1.4 实数的连续性
现在,数轴上有了整数、有理数、无理数了,数轴上还有坑吗?没有了。怎么证明?呃,这个证明虽然不复杂,但是有点烧脑,跳过吧,不妨碍后面的讲解。
整数、有理数、无理数统称为实数,实数是连续的。直观理解连续,就是数轴上没有坑了,再也不可能有别的数了。实数的连续性是非常重要而且基础的性质,没有实数连续性,函数就不连续,函数不连续,可微可导微积分都没有了,真不知道世界会是什么样子。
再比如,我们想想,有理数是一个个的点,长度为0,就算无数多个有理数加起来,长度还是为0,那么长度是哪里来的?连续的实数才有长度,怎么证明?也无法证明,这是关于连续性的一种性质。至此,我们把实数称为”完备“。
当然,还有人说,我可以不破坏实数的各种性质,但是可以在实数的缝隙里面加上无穷小量(在上面的实数理论中,无穷小量不是确确实实的数,只是一个概念),就这么创造了新的实数,这种实数自有它的用处,不过目前不是主流。
1.5 数学并非科学
什么是科学?科学很重要的一点是,可以被证伪。比如说我们说水的沸点是100摄氏度,那到底是不是呢?用温度计量了就知道。科学的研究需要用事实来证明或者证伪。
从实数理论来看,我们可以认识到一点,数学并非科学。比如上面说的无穷小量到底是不是数,就可以被随意的定义了,在这个基础上,没有逻辑矛盾的推出了各种理论理论,自然也没有办法证明和证伪。
所以数学会从各种公理出发建立很多分支,不过如果和科学研究脱钩的话,这个分支也不会有很多人去研究它,慢慢也就失去了活力。当然也有很多分支本来也只是少数数学家的玩具,后来被发现可以作为工具进行各种数学研究。现在可能最纯粹的数学只有”数论“了。
想起一个爱因斯坦的公案,爱因斯坦作为一个理论物理学家,工作方式很像是一个数学家,从光速不变这个假设出发,推出了”相对论“,学术界都说,你好牛哦,说的好有道理哦,但是,诺贝尔物理学奖没有办法颁给他,因为证明不了也证伪不了!颁奖委员会当时的心态是”我好想给爱因斯坦颁奖哦“,就在爱因斯坦的研究中找个靠谱的”光电效应“颁奖。
2 虚数是否真是存在?
虚数这个名字,指出了一点,虚数在现实中没有对应物的,是一个人工数。似乎是人工数就必然不真实,让我们来看看是不是?
2.1 虚数开始是数学家的玩具
古代的数学家也和我们一样,也玩24点,意大利米兰有个数学家叫做卡当,出了一个题,能否把10分成两部分,让它的乘积为40?他给出的答案是,$\left(5+\sqrt{-15}\right)\left(5-\sqrt{-15}\right)=40$ ,这里负数第一次出现在了根式里,不过就好像几何题划的辅助线一样,虽然参与运算,但是并没有意义。数学家也不可能给辅助线专门定义一个概念。
2.2 虚数似乎没有充分存在的理由
虚数 $i=\sqrt{-1}$ ,这个就是i 的定义,听它的名字就感觉它是“虚”的:
- 从自然数扩张到整数:增加的负数可以对应“欠债、减少”
- 从整数扩张到有理数:增加的分数可以对应“分割、部分”
- 从有理数扩张到实数:增加的无理数可以对应“单位正方形的对角线的长度($\sqrt2$)
- 从实数扩张到复数:增加的虚数对应什么?
虚数似乎只是让开方运算在整个复数域封闭了(即复数开方运算之后得到的仍然是复数)。看起来我们没有必要去理会 $\sqrt{-1}$ 到底等于多少,我们规定 $\sqrt{-1}$ 没有意义就可以了嘛,就好像 $\frac{1}{0}$。我们来看一下,一元二次方程$ax^2+bx+c=0\left(a\neq0\right)$ 的万能公式:其根可以表示为:
$$ x= \frac {-b\pm\sqrt {b^2-4ac}}{2a} $$
,其判别式$\Delta=b^2-4ac$ 。
- $\Delta>0$有两个不等的实数根
- $\Delta=0$有两个相等的实数根
- $\Delta<0$有两个不同的复数根,
其实规定为无意义就好了,干嘛理会这种情况?数学家很吝啬的,不会为这点微不足道的好处去增加概念。虚数如果只是让开方可以封闭,运算出来的结果还是虚数,这个理由不充分。对于数学而言,概念、公理越少越好,越少数学的根基就越稳固。欧式几何的五个公设,两千年来数学家都在企图去证明第五公设,只为了减少一条公设。
2.3 虚数是解一元三次方程的必须工具
我们再看一下,一元三次方程 $ax^3+bx^2+cx+d=0\left(a\neq0\right)$ ,一元三次方程的解太复杂了,这里写不下,大家可以参考维基百科,但愿大家能够打开。我们讨论一下 b=0 ,此时,一元三次方程可以化为 $x^3+px+q=0$ ,其根可以表示为:
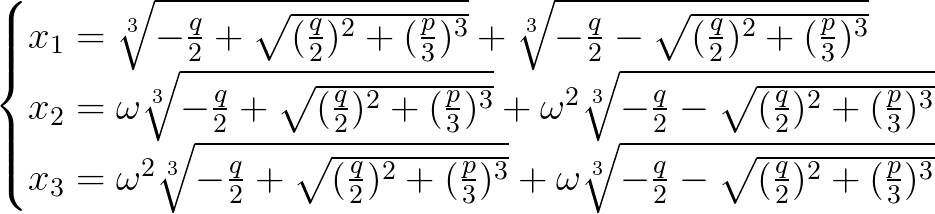
其中
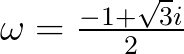
。
判别式为
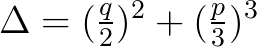
,注意观察解的形式, $\Delta$ 是被包含在根式里面的。
- $\Delta>0$有一个实数根和两个复数根
- $\Delta=0$有三个实数根,当 $p=q=0$ ,根为0,当$p,q\neq0$ ,三个根里面有两个相等
- $\Delta<0$有三个不等的实根!懵了,要通过复数才能求得实根?
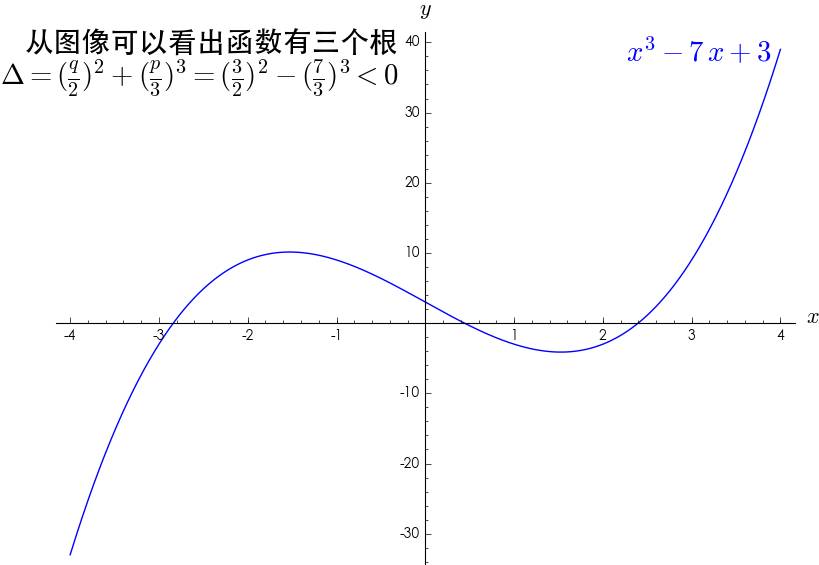
要想求解三次方程的根,就绕不开复数了吗?会不会这只是求根的方法之一?这个也被证明了,确实需要通过复数来求解实数根。求解方程组,确实让人觉得虚数是一个必要的数学工具,但是还是没有揭开它的本质,还不足以让其登堂入室。
2.4 虚数真实存在的理由
这个必须从泰勒公式的收敛性说起。泰勒公式的收敛性直观来说就是泰勒级数(即泰勒公式展开后的级数)的函数图像是否能够贴合原函数,这个和泰勒级数本身的收敛性有关。
2.4.1 $f(x)=sin(x)$泰勒展开
$f(x)=sin(x)$的收敛性在 $x=0$点泰勒展开:
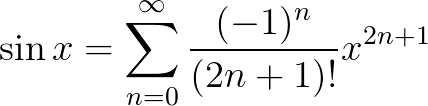
级数的收敛范围是$-\infty<x<+\infty$ ,如图,用n 来表示展开的阶数(阶数即泰勒级数里面求导的次数,或者可以理解为级数多项式的最高次数):
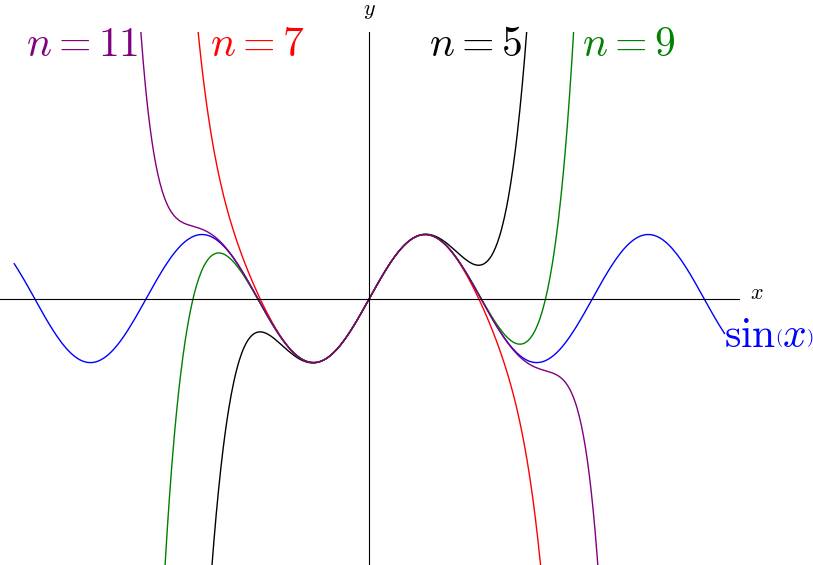
$sin(x)$ 的泰勒级数在整个实数范围收敛,展开的阶数越多,对原函数的贴合就越好。
2.4.2 $f(x)=\frac{1}{1-x}$的收敛性
$f(x)=\frac{1}{1-x}$的收敛性在 $x=0$ 点泰勒展开,
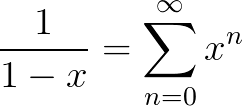
级数的收敛范围 $|x|<1$ :
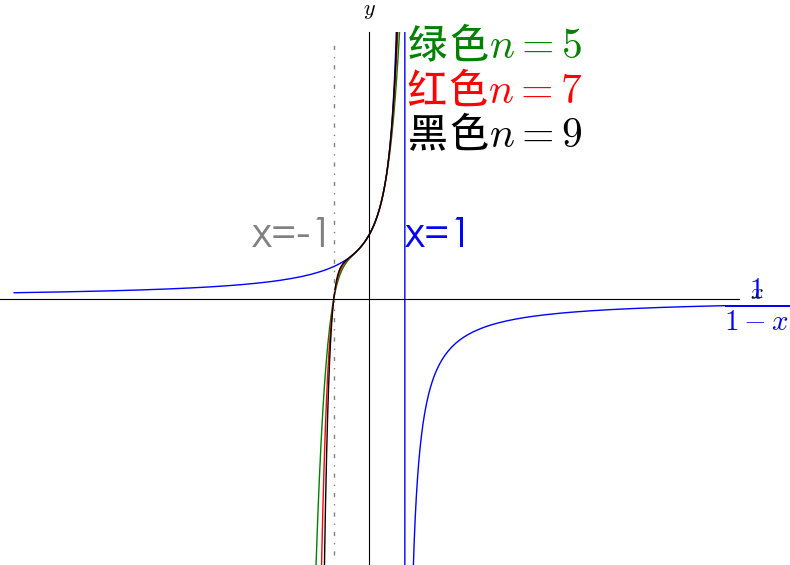
从图中可以看到,泰勒级数在 $|x|<1$ 收敛。超出这个范围,泰勒级数的图像就远离原函数的图像。
在 $x=0.5$ 点泰勒展开,
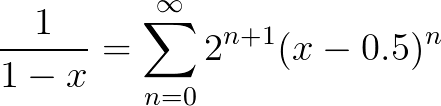
级数的收敛范围 $0<x<1$:
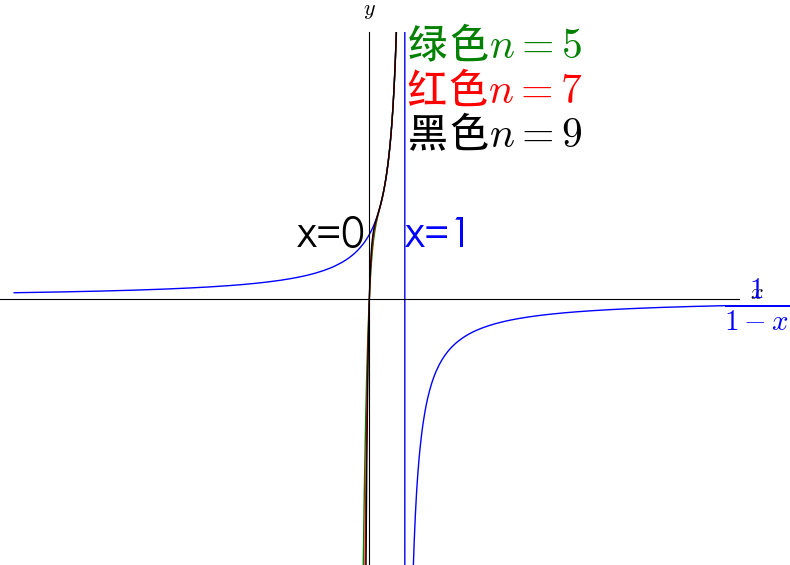
从图中可以看到,泰勒级数在 $0<x<1$ 之间收敛。超出这个范围,泰勒级数的图像就远离原函数的图像。
对比这两个展开的收敛区间,我们看不出什么特点出来,我们以收敛范围作为直径,展开点作为圆心来画下圆(这个圆被成为泰勒级数的收敛圆)看看:
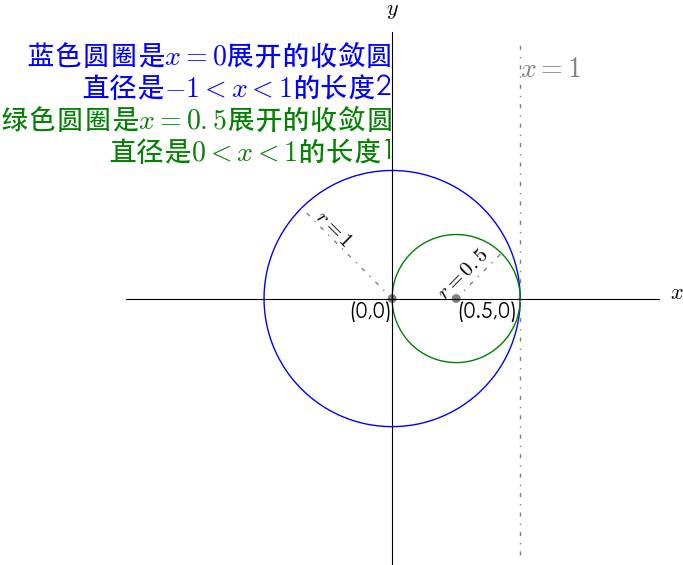
在不同位置展开的泰勒级数的收敛圆都相切于 $x=1$ 这根直线。
解释一下原因, $f(x)=\frac{1}{1-x}$ 有一个奇点,即 x=1 的话,有$\frac{1}{1-x}=\frac{1}{0}$ 没有定义,而泰勒级数的图像会以展开点为中心对称(容易验证,级数不是奇函数就是偶函数),所以如果在 $x=0$ 点展开的话,因为 $x=1$有$f(x)\rightarrow\infty$ ,所以对称的位置 $x=-1$ 有$f(x)\rightarrow-\infty$ 。同理如果在 x=0.5点展开的话,因为 $x=1$有$f(x)\rightarrow\infty$ ,所以对称的位置 $x=0$ 有$f(x)\rightarrow-\infty$ 。
数学总是有道理的对吗?
2.4.3 $f(x)=\frac{1}{1+x^2}$的收敛性
$f(x)=\frac{1}{1+x^2}$的收敛性在x=0 点泰勒展开,
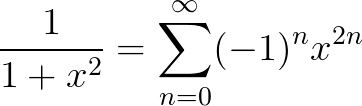
级数的收敛范围 $|x|<1$ :
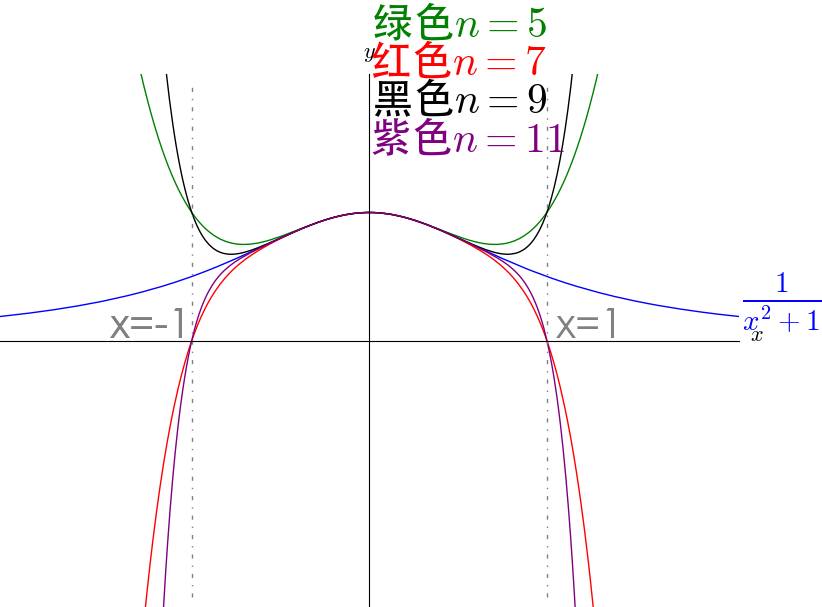
可以看出, $\frac{1}{1+x^2}$ 很奇怪的在 $|x|<1$ 收敛,可是 $\frac{1}{1+x^2}$ 本身并没有奇点啊?
在 x=1 点泰勒展开,级数的收敛范围 $1-\sqrt2<x<1+\sqrt2$ :
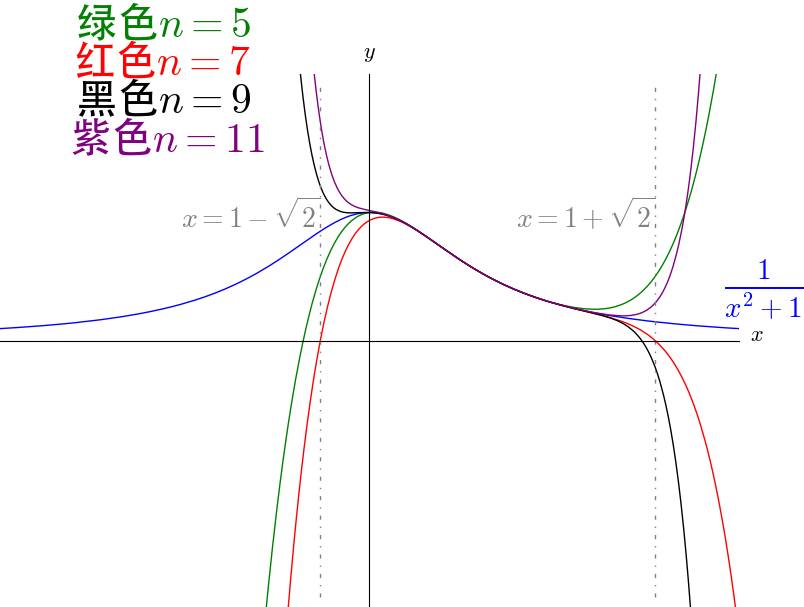
可以看出, $\frac{1}{1+x^2}$ 在 $1-\sqrt2<x<1+\sqrt2$ 收敛,仍然很奇怪。
对比这两个展开的收敛区间,看不出什么规律来,同样的画下收敛圆看看:
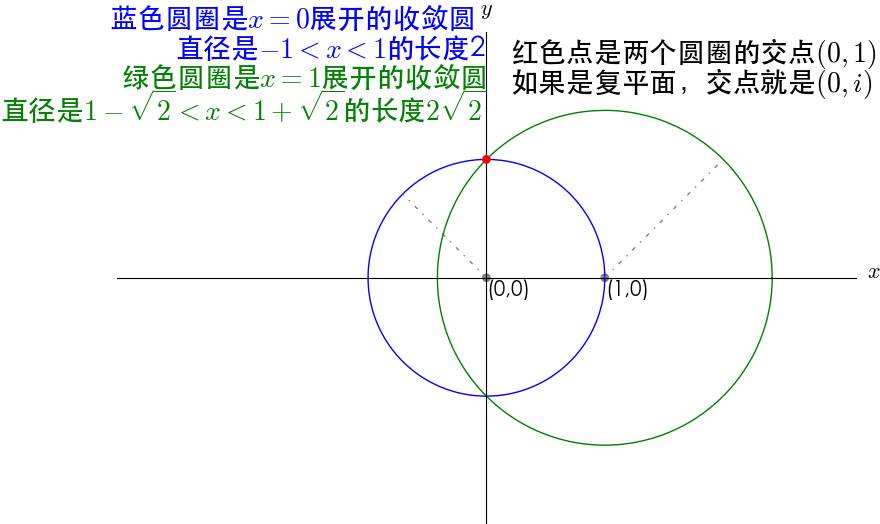
注意两个圆的交点是 (0.1), 或者放到复平面上去就是 (0,i) 。这并不是巧合,确实是和虚数有关。
很长时间数学家都不知道为什么 $\frac{1}{1+x^2}$ 收敛范围这么奇怪,直到虚数出现之后,大家才知道x=i 的话,有$\frac{1}{1+x^2}=\frac{1}{0}$ 是个奇点!
整个推论过程从头到尾就没有出现过i 的身影,最后却不得不考虑i 。泰勒公式也使得数学家不得不认真面对虚数这个问题。
数学还是很讲道理的对吗?
泰勒公式的收敛性不得不让我们这样去考虑问题,虚数是真实存在的。我们长期习惯了用实数去思考数学问题,直到我们发现实数只是真实存在的复数的一部分。把实数比作三维空间,复数就是四维空间,泰勒公式就是生存在四维空间的动物。当我们在实数范围内研究泰勒公式时,我们发现它的行为好奇怪,最后才发现原来这不过是它在三维空间的投影。
实数是复数的一部分,用实数去研究数学问题并不是说不正确,就好像用牛顿力学在微观领域没有建树,但是去研究宏观物体仍然适用一样。只是我们应该看到更大的一个世界。
3 结论
虚数是人工设立的一个概念,没有现实的对应物,但是我们不能认为它不存在,是虚构的。就好像每天我们要喝的水,我们知道他是由 $H_2O$ 组成,可是谁见过 H?究竟是什么?目前对原子的了解也只是停留在数学方程式上,到底是什么样子我们也不清楚,但是肯定不能说H不存在。
原文来自:数学控制club,公式重新整理。
