稳定性分析的一个例子
已知系统:
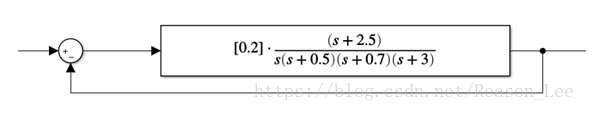
请判断其稳定性。
思路:判断系统的稳定性,只要求出系统的闭环极点即可,而系统的闭环极点就是闭环传递函数的分母多项式的根,可以利用MATLAB中的tf2zp函数求出系统的零极点,或者利用root函数求分母多项式的根来确定系统的闭环极点,从而判断系统的稳定性。同时采用阶跃响应曲线可以验证系统稳定性。
以下为基于Simulink采用阶跃响应曲线验证并观察系统稳定性。
Simulink建模如下:
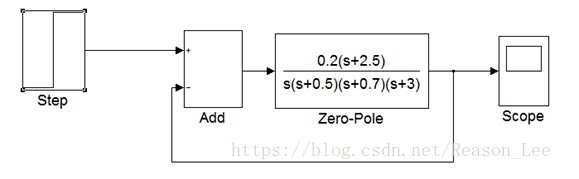
结果如下:
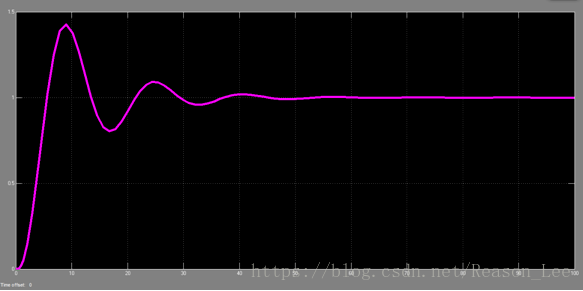
以下为基于MATLAB编程(改变系统增益K的值,观察并分析K值得改变对于系统稳定性的影响)绘制系统零极点分布图分析系统稳定性:
1 | clc;clear;close all; |
结果如下:
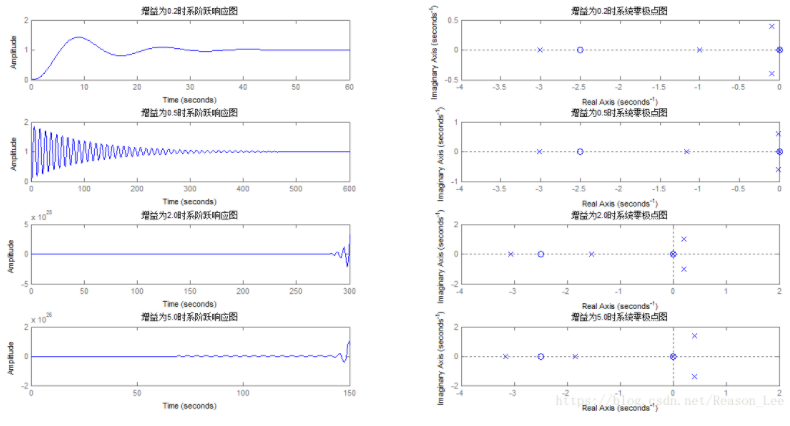
观察上图可以发现当增益小于1时,系统稳定,此时系统的所有极点都位于S平面的左半平面。而当增益大于1时,系统变得不稳定。此时系统的有极点位于S平面的右半平面。
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 ZYMIN!
