关于矩阵的理解与解释
本文总结了矩阵的理解和解释。
正定矩阵
我来说一个正定矩阵在物理上的应用。原链接
物理上有个定理叫做最小作用量原理,这是力学的基础。这个定理说,粒子总是沿着作用量极小的那条路径运动的。 作用量说白了就是粒子的动能和势能的差。大家都知道动能正比于速度的平方。但是你考虑粒子未必只有一个独立的速度分量,特别是那些由许多粒子构成的系统,可能会有成千上万个速度。所以一般来说,动能是速度的二次型。也就是说,可以写成中间一个矩阵,速度矢量夹在两边。中间那个矩阵地位与质量相当,有时就称为质量矩阵。 好了,现在我们有一个很重要的要求,就是质量矩阵必须是正定的。 为什么呢?因为正定矩阵的二次型也是正定的,也就是说最少最少也要是0. 作用量要极小化,如果质量矩阵不是正定的,那么动能就可以是负的。这样我们如果使某些速度无限地增大,动能就越来越负,作用量就没有底了,怎么极小化呢。所以质量矩阵的正定性是能够实现作用量极小的要求,一切物理上合理的系统都应该具有正定的质量矩阵。
还有一个例子,就是量子力学。原链接
量子力学的数学基础之一是Hilbert空间。Hilbert空间是一个内积空间。向量和自己的内积也是二次型,一般都是正定的。更装逼一点地说,就是Hilbert空间的度规是正定的。但是在相对论性量子力学里,我们发现Hilbert空间再也不能完备所有的波函数了,我们必须引入非定度规的线性向量空间。在非定的度规下,波函数和自己的内积可以是负的,整个量子力学的测量理论都要为此而改写。 一个向量的模方还可以是负的?不要感到诧异,这有着非常重要的物理意义,这代表了反物质的出现。描写正常物质的波函数的模方是正的,而描写反物质的波函数的模方是负的。从物理上说,反物质的出现是一种狭义相对论的量子效应,而其数学基础与度规的正定性有着密切的关系。
特征值与特征向量
设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A特征值,非零向量x称为A的对应于特征值λ的特征向量。式Ax=λx也可写成( A-λE)X=0。这是n个未知数n个方程的齐次线性方程组,它有非零解的充分必要条件是系数行列式| A-λE|=0。
特征值就是运动的速度,特征向量就是运动的方向。
行列式的本质是什么
行列式是线性变换的伸缩因子。线性变换的几何直观有三个要点:
- 变换前是直线的,变换后依然是直线
- 直线比例保持不变
- 变换前是原点的,变换后依然是原点
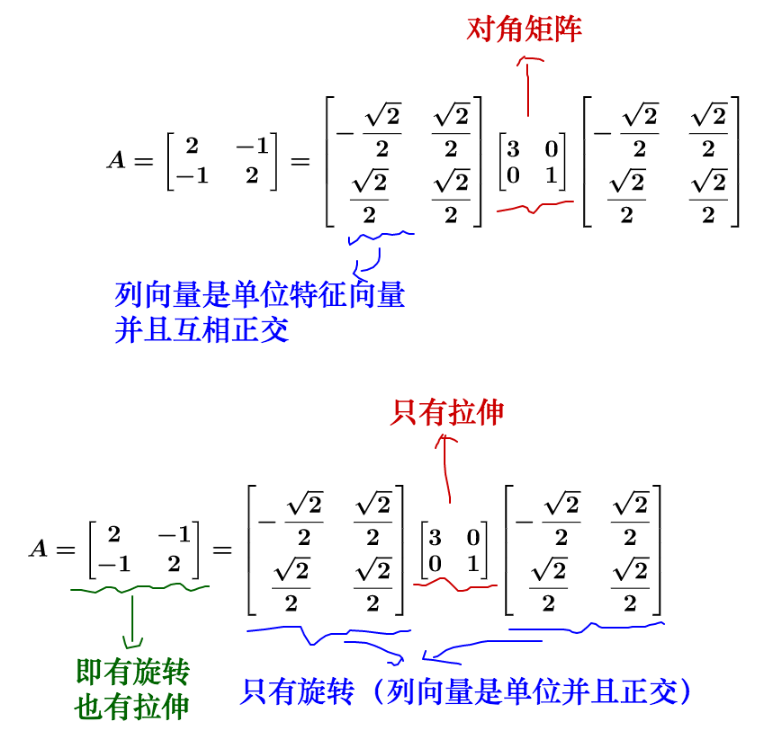
线性变换可以看做是对基的变换。
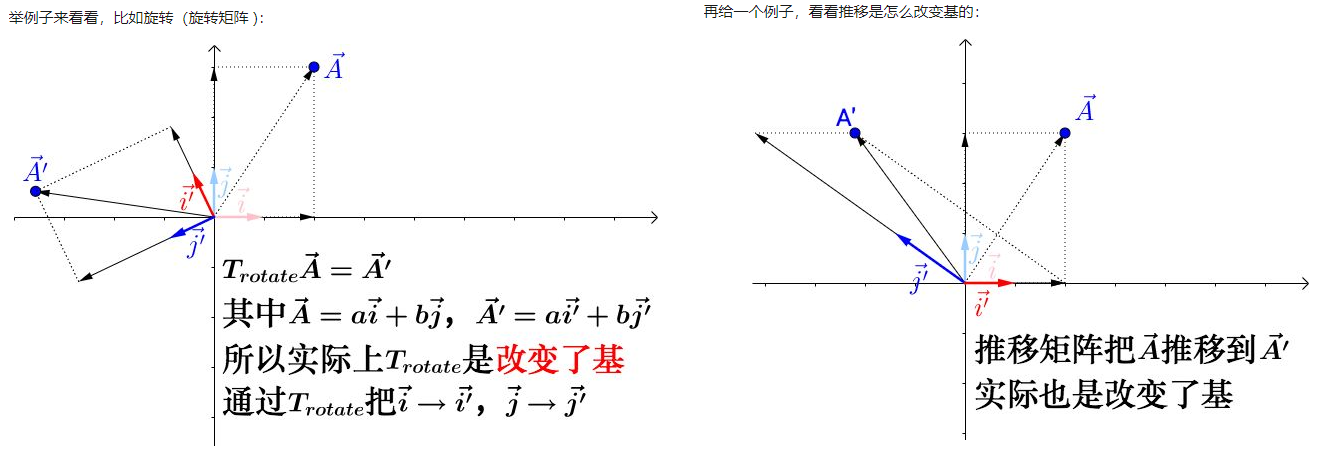
行列式是线性变换的伸缩因子。
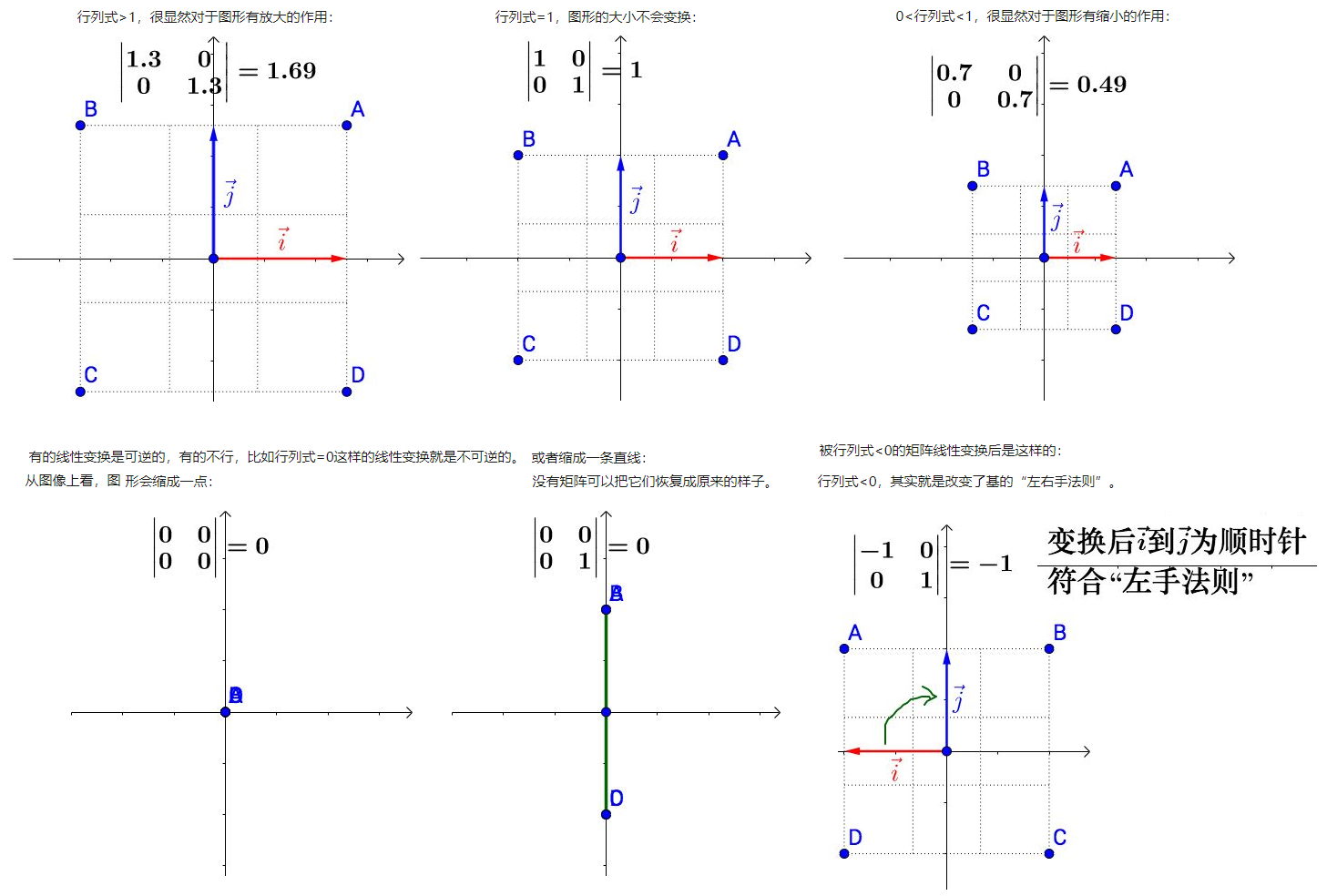
特征值与奇异值
特征值分解和奇异值分解(SVD)在主成分分析(PCA)和机器学习领域都有广泛的应用。PCA的实现由两种方法,一种是特征值分解,另一种是奇异值分解,特征值分解和奇异值分解的目的是一样的,都是提取出一个矩阵最重要的特性。特征值和奇异值都有其特定的物理意义,如奇异值分解可以将一个复杂的矩阵分解成几个小且简单的矩阵相乘,这些小矩阵就包含的矩阵的重要特性(奇异值、左右奇异值向量等)。
有人在博文中用“描述一个人”的例子来解释过奇异值分解:“描述一个人说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力。”其中的“人脸上的特征有着无数种”就构成了待分解的矩阵,“寥寥得几个特征”代表了分解后的几个小矩阵,“人天生的抽取能力”就是一个奇异值分解(SVD)的过程。说了这么多关于奇异值分解的物理意义,接下来将依次介绍特征值和奇异值的相关知识。
对特征向量x进行A变换的实质是将特征向量进行缩放,缩放因子为特征值λ。因此,特征向量的代数上含义是:将矩阵乘法转换为数乘操作;特征向量的几何含义是:特征向量通过方阵A变换只进行伸缩,而保持特征向量的方向不变。特征值表示的是这个特征到底有多重要,类似于权重,而特征向量在几何上就是一个点,从原点到该点的方向表示向量的方向。
一个变换方阵的所有特征向量组成了这个变换矩阵的一组基。所谓基,可以理解为坐标系的轴。我们平常用到的大多是直角坐标系,在线性代数中可以把这个坐标系扭曲、拉伸、旋转,称为基变换。我们可以按需求去设定基,但是基的轴之间必须是线性无关的,也就是保证坐标系的不同轴不要指向同一个方向或可以被别的轴组合而成,否则的话原来的空间就“撑”不起来了。
从线性空间的角度看,在一个定义了内积的线性空间里,对一个N阶对称方阵进行特征分解,就是产生了该空间的N个标准正交基,然后把矩阵投影到这N个基上。N个特征向量就是N个标准正交基,而特征值的模则代表矩阵在每个基上的投影长度。特征值越大,说明矩阵在对应的特征向量上的方差越大,功率越大,信息量越多。
总结一下,特征值分解可以得到特征值与特征向量,特征值表示的是这个特征到底有多重要,而特征向量表示这个特征是什么,可以将每一个特征向量理解为一个线性的子空间,我们可以利用这些线性的子空间干很多的事情。不过,特征值分解也有很多的局限,比如说变换的矩阵必须是方阵。
在机器学习特征提取中,意思就是最大特征值对应的特征向量方向上包含最多的信息量,如果某几个特征值很小,说明这几个方向信息量很小,可以用来降维,也就是删除小特征值对应方向的数据,只保留大特征值方向对应的数据,这样做以后数据量减小,但有用信息量变化不大,PCA降维就是基于这种思路。
特征值及特征值分解都是针对方阵而言,现实世界中,我们看到的大部分矩阵不是方阵,比如每道数据有M个点,一共采集了N道数据,这样就形成了一个N*M的矩阵,那么怎样才能像方阵一样提取出它的特征,以及特征的重要性。奇异值分解就是来干这个事情的。奇异值相当于方阵中的特征值,奇异值分解相当于方阵中的特征值分解。
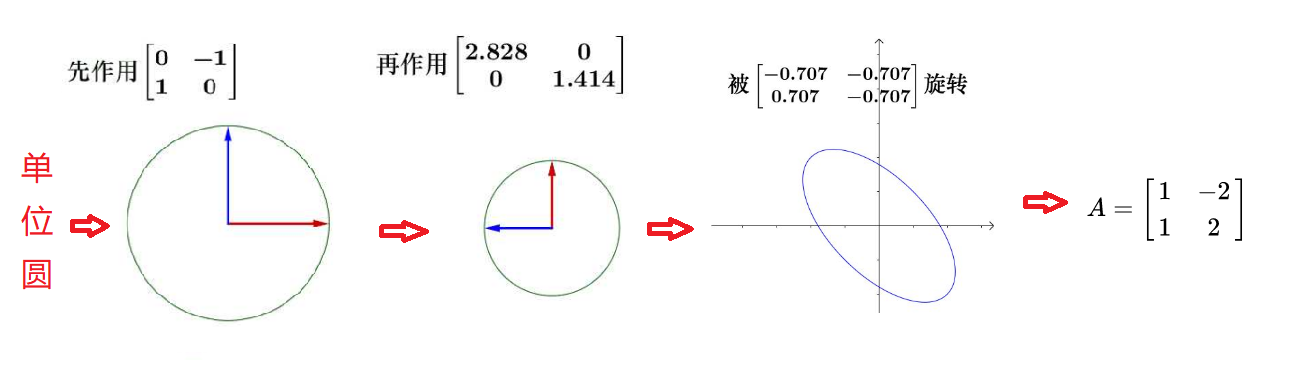
奇异值分解是一种适用于任意矩阵的分解方法。 这就表明任意的矩阵 A 是可以分解成三个矩阵相乘的形式。V表示了原始域的标准正交基,U表示经过A 变换后的co-domain的标准正交基,Σ表示了V 中的向量与U中相对应向量之间的关系。我们仔细观察上图发现,线性变换A可以分解为旋转、缩放、旋转这三种基本线性变换。
奇异值分解实际上把矩阵的变换分为了三部分:旋转、拉伸、投影。拿刚才的:$A=\left[\begin{matrix}1 &-2 \1 &2\end{matrix}\right]$举例子(方阵没有投影,不过不影响这里思考):