机器人动力学概述
提到动力学,我们的第一印象往往是几行甚至几百行的公式,大部分对动力学感兴趣的朋友可能会因此而止步不前,实际上动力学要比纯粹的公式生动丰富的多。为使读者对动力学控制器有个直观而又全面的了解,作者仅概略性地总结包括动力学定义、应用范围、建模方法、具体部署方式及评价标准在内的方方面面。
动力学定义
动力学(dynamics)是研究作用于物体的力和物体运动之间的一般关系,具体到工业机器人,它包括两个基本问题:
1). 已知作用在机器人各关节的力,求该关节对应的运动轨迹,即求加速度,速度和位置;
2). 已知机器人关节当前的加速度,速度和位置,求此时关节上的受力大小。
简单讲,动力学是解决机器人各关节受力大小和它运动之间的关系,已知运动的特性能够求出对应的力的大小,反之,已知受力的大小,可以计算出机器人的运动特性。


动力学模型/方程
动力学的计算有很多方法,如Lagrange、Newton-Euler、Gauss、Kane、Screw、Roberson-Wittenburg。其中以Lagrange、Newton-Euler最为常用。实际上这些方式建立的动力学模型最终是可以互相转化的。我们以在竖直平面内运动的二连杆机器人为例,先观察一般的动力学模型都由哪些项组成,在直观上对动力学有一个认识。观察竖直平面内运动的二连杆机器人动力学模型可以发现,采用拉格朗日方法建立的动力学模型,最终都可以用如下标准的形式来表示。
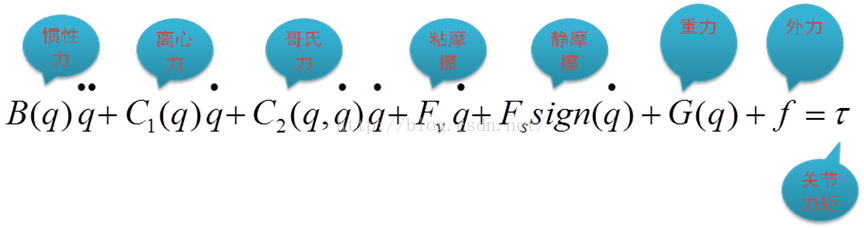
标准的动力学模型若纯粹以力的形式来表达,即其是由惯性力,离心力,哥氏力(又称科里奥利力),粘摩擦力,静摩擦力,重力,外力(如人工施加或与环境接触),关节力矩组成一系列等式。需要说明的是此处的摩擦力模型为:粘摩擦+库伦摩擦,采用不同摩擦力模型,上述方程仅在摩擦力这一处有所不同,其余不变。
除科里奥利力以外,其他几个力均相对容易理解。那么科里奥利力在我们生活中的表现是什么?细心的读者在生活中可能会发现,河流的两侧被河水冲刷的情况不一致。还有一个被称为“物理学最美实验之一”的傅科摆,也是受到科里奥利力的影响。地球上引起科里奥利力的本质原因是处于不同维度的地方自转速度不同,而针对机器人,不同关节其转速不同,同样会引起科里奥利现象。
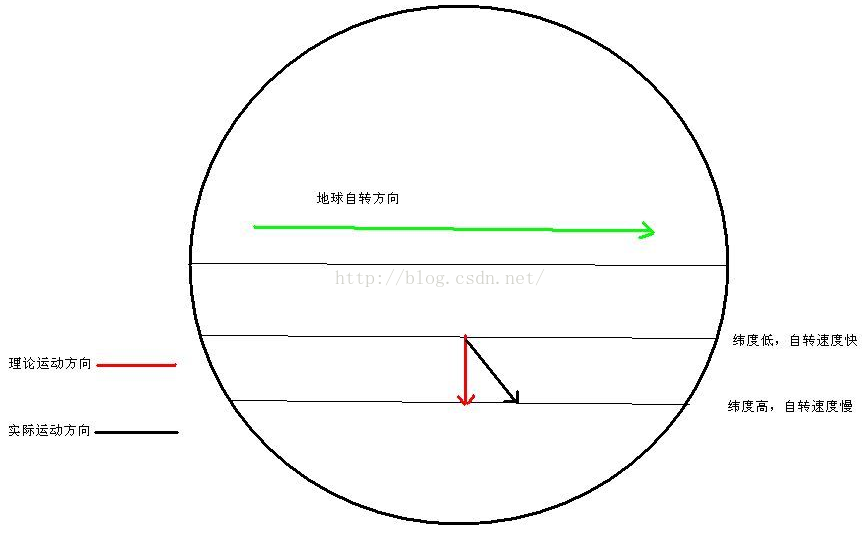
附:傅科摆
在地球上的摆动会受到地球自转的影响。只要摆面方向与地球自转的角速度方向存在一定的夹角,摆面就会受到哥氏的影响,而产生一个与地球自转方向相反的扭矩,从而使得摆面发生转动。 1851年法国物理学家傅科预言了这种现象的存在,并且以实验证明了这种现象,他用一根长67米的钢丝绳和一枚27千克的金属球组成一个单摆,在摆垂下镶嵌了一个指针,将这个巨大的单摆悬挂在教堂穹顶之上,实验证实了在北半球摆面会缓缓向右旋转 。
动力学控制器的部署方式
基于动力学模型的控制器,具体实现方式因系统结构不同而有所不同。针对驱控一体的控制器架构,我们可以采用“计算力矩(compute torque)”的控制方式;而针对以总线型分布式控制结构的系统,将经(正向?,逆向?)动力学计算出的力矩,以前馈的方式,加入到伺服的电流控制环路,完成动力学控制器的设计,如下图 以力矩前馈方式实现的动力学控制器。需要说明的是,针对那些不支持力矩前馈的伺服,可通过速度前馈甚至位置前馈的方式来实现动力学控制器。
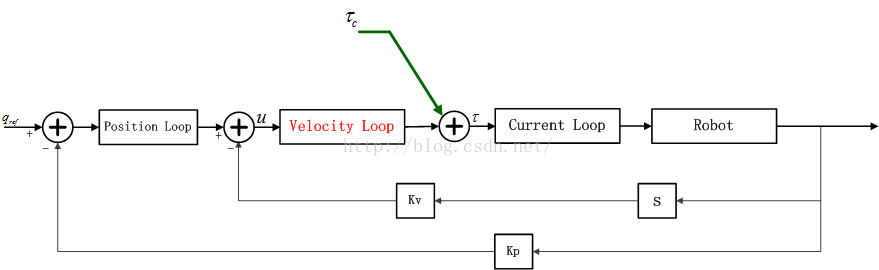
控制方式
运动控制
机械手任务:在工作空间执行特定的运动和接触力。
运动控制目的:确定由关节执行元件所形成的广义力,保证实现任务的同时,满足给定的瞬态和稳态要求。
两种控制方案:关节空间控制和操作空间控制。关节空间的控制先通过逆运动学解算出各个关节的运动,然后用真实运动来跟踪参考输入。操作空间的控制采用真题求法,运算更复杂,而且末端操作器的位姿难以直接测量得到。

力控制
前提:机械手与外部环境有交互力。在交互作用中,环境会对末端执行器的路径产生约束。
背景:在任务准确规划的前提下,才能通过运动控制实现与环境的交互任务。这需要机械手(运动学和动力学)和环境(几何特征、机械特性)的准确建模。对环境建模十分困难。
在力控制中,如果关节没有柔性,可能破坏机械臂执行元件或与机械手接触的环境。
阻抗控制:建立一个期望的机器人位置和接触力的动态响应关系。将外界环境系统视为对机器人系统的一种“干扰”,并给机器人在受外界力而偏离既定运动时具有阻抗形式的扰动响应。通过改变上述阻抗,就可以调节机器人与外界的动态作用。

