此次的笔记主要是介绍背景知识，这里将整理一些后续设计神经网络控制器需要用到的一些知识储备，包括系统的类型，不同的表达方式，属性（如利普西斯条件），连续、一致连续的概念和理解等；还有很重要的一点是，也会记录利用matlab编写系统仿真的流程。

1. 系统分类

系统分为两大类，①自治系统（autonomous system）$\dot{x}=f(x)$和②非自治系统（non-autonomous system）$\dot{x}=f(x,t)$。如果认真看的话，不难发现，这两种系统仅有一个地方不同，就是非自治系统在系统模型上，是关于时间t 的显性表达（在英文文献中的explicit time dependence就是这个意思）。

简单粗暴的从中文译文的意思来看，就是说自治系统自我管理，不收外界的干扰，非自治则是受外界干扰生活不能自理，这种生活不能自理的人，当然是很难管教的。自治系统的系统结构和参数是不会随着时间的变化而有所改变的，对于这样的一个系统，给定了输入和已知初始状态，其系统的输出是完全可以确定下来的，因此这样的系统控制起来也相对，注意只是相对更简单些。

而非自治系统就麻烦许多，因为系统的结构和参数是时变的，系统的输出除了依赖于系统的初始状态和控制量输入（control input）外还要依赖于时间，因为不同的时间下，系统的参数不同，即系统某个量的具体取值是关于时间的函数。这样的系统极其麻烦，比如系统的模型上考虑了外部干扰的影响，增加了d(t)项，那么该系统就是个非自治系统了。这时候我们也可以简单地说，自治系统是时不变系统（time invariant）而非自治系统则可以简单理解为时变系统（time-varying）。

那么我们该如何认识这两者的关系？我个人认为自治和非自治系统相当于线性系统和非线性系统的关系，非自治系统和非线性系统是自治系统和线性系统的一般化，更加贴近实际，然而也更加难分析和控制，试想机械器件是肯定会发生老化、磨损等的，其中相关的参数会随着时间不断变化，从这个角度看，系统是非自治系统，但在短时间内，这些参数的变化可以忽略，并不影响控制性能，可以近似看作是自治系统。这相当于非线性系统在工作点附近可以近似线性化处理，利用线性理论的工具解决问题。下面我们主要围绕自治系统进行讨论分析。

2. 预备知识

问题的分析总是要由浅入深的，因此，我们首先讲述的是自治系统的相关知识。我们再次写出自治系统的表达式：$\dot{x}=f(x)$。可见该系统表达成了一阶微分方程的形式，之所以这么写，是因为，任意高阶的表达系统动力学模型的微分方程组，都可以用一阶微分方程表达，因此在分析一类系统的时候，研究学者都热衷于从一般形式的系统出发，推出定理。x是系统的状态变量，一般用列向量表示，而f 则是向量函数。下面我们来介绍回忆一下一些基础数学知识：

  • 向量和矩阵范数

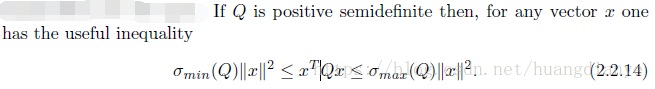
  • 连续性和函数范数
    关于连续的定义如下：

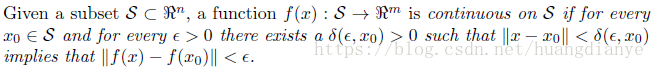
最通俗的理解就是，函数曲线能够一笔画完的就是连续的函数，如果要分段且不是光滑过度的函数曲线就是不连续曲线。由函数的连续性可以引伸出巴巴拉引理barbalet如下，巴巴拉引理告诉我们当一个函数积分有界，且该函数是一致连续时，那么该函数随着时间的推移，趋于零。该引理可以迁移到Lyapunov函数的分析上，往往能够简化对半负定的情况的分析过程。

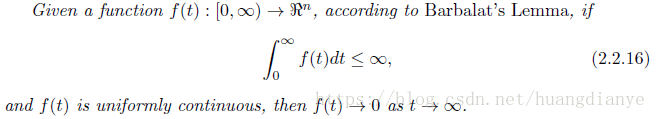
有一个常用性质是利普西斯条件，利普西斯条件实际上就是函数输入量发生变化导致的函数值变化有限，且这种变化存在一个上界常数。

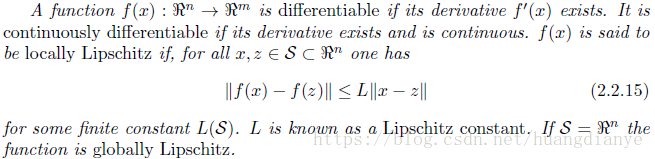
函数范数

动态系统的分析设计中需要考虑到稳定性问题，Lyapunov的稳定性分析方法在前面的问题中已经讨论过了，但前面并没有包含一致最终有界的情况(UUB uniformly ultimately bounded)，这种稳定性在神经网络分析中经常用到，可以当做是利用神经网路的逼近性质去补偿系统的不确定项的时候的残差进行分析的一种稳定性分析过程。

UUB简要的描述就是，在集合S内的初始状态，在有限时间T（与初始状态和界限相关）内，最终收敛到平衡点的有界B附近。

UUB与SISL（stable in sense of Lyapunov）的区别在于，系统收敛时，系统初始状态到平衡点的距离范数是有界的，而不是任意靠近的。这种假设更具有实际意义。SISL的稳定则是要求系统能够通过设置初始状态任意靠近平衡点。（Note that for SISL there is a requirement that the state x(t) be kept arbitrarily close to x_e by starting sufficiently close to it.）

  • 利用UUB进行Lyapunov分析

不难理解上述定理，就是在R外的半径L的斜率是负定的，注意一定是负定的，如果是半负定可能会落在外部的极限环中，而在R的内部，L的一阶导可以是正定的。这样在一定程度上弱化了对控制器设计的要求，使控制器更具现实意义。

3.系统表示

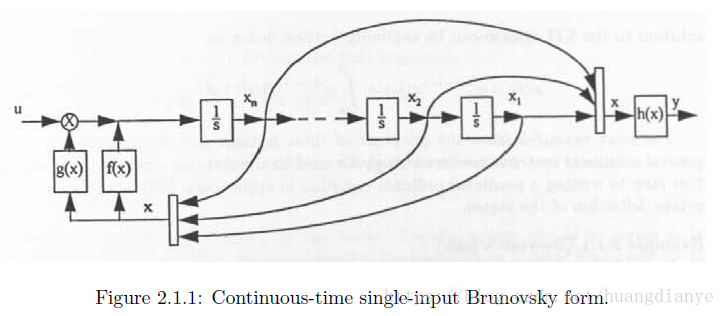
对于任意阶的微分方程组，可以化为用向量表示的而解方程组。Brunovsky Canonical Form

该形式通过串联积分块再进行反馈

4. 仿真程序的构建

对一个系统进行仿真编程，要考虑该系统的表示方式是连续形式亦或是离散形式，对于一个连续系统，需要使用ode23或更高阶的ode45求解器对微分形式进行求解，然后输出模型状态，而对于离散形式，则只需要自行搭建一个for loop分步仿真。当然仿真也还有其他方法，如使用simulink搭建，利用s-function进行微分方程的求解等。

matlab程序编写如下

4.1连续系统的仿真程序
①需要构建一个function文件
②在脚本中调用function文件
③plot仿真图像
function文件的函数名编写有一定的规范，输出是状态变量的一阶导，而函数输入则是初始状态和仿真的起始结束时间构成的1\times 2 矩阵。例如：

1
2
3
function xdot= vdpol(t,x)
alpha= 0.8; u= 0;
xdot= [x(2) ; alpha*(1-x(1)^2)*x(2) - x(1) + u];123

控制器设计好后可以直接书写在该函数中。

脚本函数书写的内容为调用上述文件，并输出仿真结果，作图。

1
2
3
4
5
6
7
8
9
10
11
12
13
t0=0 ; tf= 50; % time horizon
x0= [0.1 ; 0.1]’; % initial conditions
[t,x]= ode23(’vdpol’,[t0,tf],x0);
% Time History Plot:
plot(t,x)
title(’Van der Pol Oscillator Time Histories’)
xlabel(’time (sec)’)
ylabel(’states x1(t) and x2(t)’)
% Phase-Plane Plot:
plot(x(:,1),x(:,2))
title(’Van der Pol Oscillator Phase Plane Plot’)
xlabel(’x(1)’)
ylabel(’x(2)’)12345678910111213

4.2 离散系统的仿真程序
离散系统的则相对简单，只需要直接在循环中分步执行程序便可。

1
2
3
4
5
6
7
8
% Discrete-Time Simulation program for Compound Interest Dynamics
d= 100; i= .08; % 8% interest rate
x(1)= 1000;
for k= 1:100;
x(k+1)= (1+i)*x(k) + d;
end
k=[1:101];
plot(k,x)12345678

总结

这篇博文主要讲的是内容有，自治系统和非自治系统的区别，后续控制器常用的一些数学预备知识，其中需要特别留意的是UUB lyapunov analysis，最后还介绍了如何在设计好控制器后使用matlab脚本和函数文件如何进行仿真的简单步骤。