鲁棒H正无穷原理
鲁棒指系统在不确定参数(parameter uncertainties)摄动下,系统维持其自身某种性能(稳定、某指标)的特性。鲁棒性的主要问题是高频的未建模动态。应该注意的是,我们在进行鲁棒稳定性分析时,要将干扰与控制输入置0。
标准鲁棒控制问题的一般模型(双端子模型)即下线性分式变换形式:一般性描述
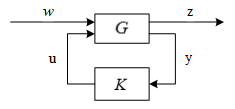
G为增广控制对象;K控制器;u是控制输入;y是被测量输出或对象输出(u和y分别是系统传递函数或者状态空间里的输入和输出);w是外部输入或参考输入,如:扰动、噪声;z是被控制的输出。
H∞控制
H指的是希尔伯特(Hilbert)空间,向量的∞范数即是最大的那个元素。 H∞是对传递函数增益大小的一个度量指标,简单说就是一个系统输入输出的放大倍数。H∞控制指的就是抑制从噪声到期望输出之间的传递函数的增益,从而使得噪声对结果的影响最小化。H无穷的标准问题实际是:求解已真有理(解析有界)的控制器K,使外输入W到加权输入Z的传递函数阵的H无穷范数最小。翻译过来就是,由于我们一般考虑线性系统,直接运用闭环系统稳定性分析的LMI进一步公式推导,直至导出矩阵元素中含有某一参数(性能指标)的LMI,运用MATLAB 求解即可。
灵敏度S的无穷范数可以表征扰动w对输出y的传递作用,S无穷小于1,则y对w一致衰减,系统的抗干扰能力比较好。补灵敏度T的无穷范数可以表征输入r对输出y的影响,T无穷小于1,则可以保证系统的动态性能和稳定性。综合考虑两者,通常各自加一个加权阵W1.W2 。H无穷控制实际上是一种最优控制,即使得目标函数取得极值。标准H无穷问题构造了一个广义被控对象,这个被控对象可以是传递函数形式,也可以是状态空间形式。H无穷范数小于1,可以等价于基于状态方程的黎卡提方程有解。
鲁棒H∞控制
指的是当系统参数存在一定范围内的摄动时(注意此时其传递函数非固定值,而是在一定范围内波动),系统可用一族传递函数来描述,称为传递函数集(无穷多个元素),其输入输出增益也非固定值,但我们可以选择其中最大的增益作为该函数集的增益。类似(1),鲁棒H∞控制就是抑制噪声到期望输出之间的传递函数集的最大增益,从而达到抗扰的目的。
评价:鲁棒H∞控制其实具有较强的保守性,因为它关注的是最差情况下的增益最小化,而实际情况未必是“最差情况”,理论上来说实际情况是最差情况的概率为零(但不等于不会发生)。
Matlab提供了很多H∞设计函数,与H∞设计相关的几个重要的工具箱有:Control System Toolbox,mu-Analysis and Synthesis Toolbox(mu-tools),Robust Control Toolbox(RCT)和LMI Control Toolbox。Matlab7.0之后的版本中,LMI和mu-tools都包含在RCT v3.0.1中,Matlab 7.0之前的版本中这些工具箱是独立的。
